제가 지금까지 개발자로 커리어를 쌓아 왔지만 사실 저의 전공은 수학이었습니다. 학부생 시절 수강했던 강의 중 인상깊었던 과목 중 하나로 조합론 수업을 꼽을 수 있는데요. 현재까지도 개발자로 일하며 알고리즘 관련해서는 해당 수업의 영향을 크게 받고 있다고 생각합니다.

1. Tiling

수학에서 타일링(tiling)이란 다차원의 표면을 작은 조각들로 덮는 방법을 말합니다. 여기서는 길이 n의 직사각형 막대를 일정한 크기의 직사각형 타일로 채우는 경우만을 다루려고 합니다.

1.1 Fibonacci Number

먼저 길이가 n인 막대를 1x1, 1x2 크기를 가진 타일로 채우는 상황을 생각해봅시다. 예를 들어 n=4인 경우 아래 5가지 경우의 수가 있습니다.

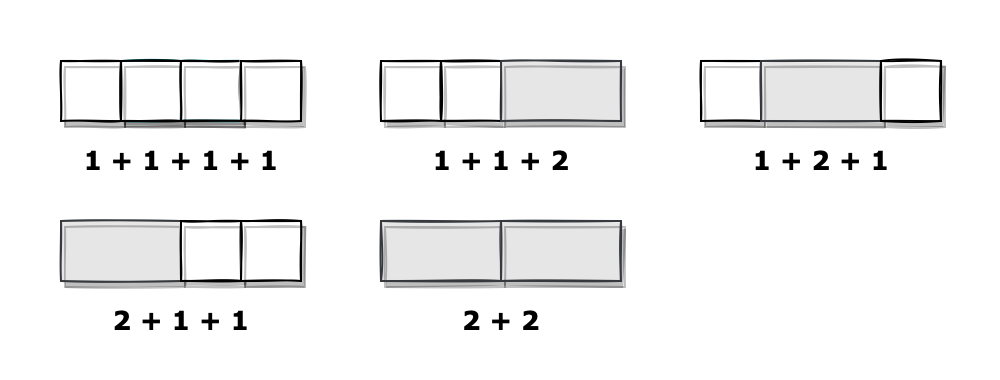
이때, 모든 경우의 수는 반드시 첫번째 타일의 길이가 1 혹은 2로 시작하는 두 가지 경우로 나누어집니다. 먼저 첫번째 타일의 길이가 1인 경우는 3가지인데 이는 뒤의 길이 3의 막대를 채우는 경우의 수와 동일합니다. 마찬가지로 첫번째 타일의 길이가 2인 경우는 나머지 길이 2의 막대를 채우는 경우의 수 2와 동일합니다.

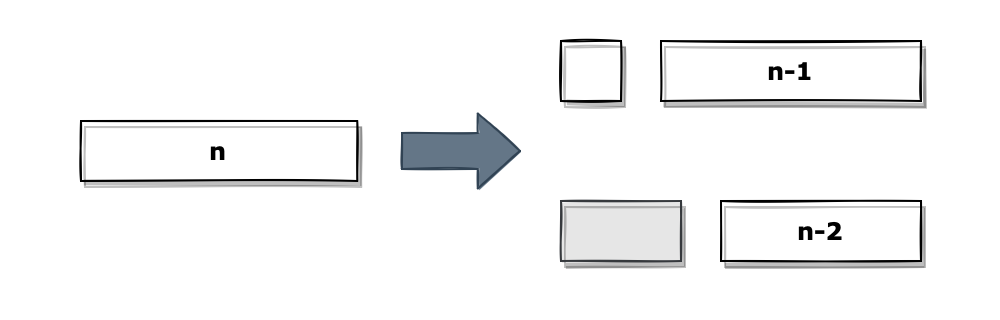
이처럼 길이 n-1, n-2의 타일을 채우는 경우의 수를 알 수 있으면 해당 두 값을 더하는것 만으로 길이가 n인 타일의 경우의 수를 구할 수 있습니다. 길이가 n인 막대를 채우는 경우의 수를 f_n 이라고 할 때 아래와 같은 공식이 성립합니다.

f_n = f_n-1 + f_n-2

아마 위와 같은 등식을 보고 피보나치 수열을 떠올릴 수 있을겁니다. f₀ = 1, f_-1 = 0이라고 하면 f_n은 완전히 피보나치 수열을 따르게 됩니다. 피보나치 수열의 일반항을 F_n라고 할 때 아래 등식이 성립합니다.

f_n = F_n+1

n=1	n=2	n=3	n=4	n=5	n=6
1	11 2	111 12 21	1111 112 121 211 22	11111 1112 1121 1211 2111 122 212 221	111111 11112 11121 11211 12111 21111 1122 1212 1221 2112 2121 2211 222
f₁ = 1	f₂ = 2	f₃ = 3	f₄ = 5	f₅ = 8	f₆ =13

1.2 Identites

위에서 정의한 f_n을 바탕으로 아래 등식을 증명할 수 있습니다.

f_m+n = f_mf_n + f_m-1f_n-1 (for m, n ≥ 0)

흔히 수학에서 증명이라 함은 수식적으로 풀어서 해결하였지만, 조합론에서는 양 변의 타일링을 가정하여 서로 완전히 대응되는지를 확인합니다.

먼저 좌변은 m+n 타일링으로 가정합니다. 우변의 경우는 m+n 타일링을 두가지 케이스로 나누어 생각할 수 있는데, m번째 위치에서 나눌 수 있는지 아니면 나누어지지 않는지 입니다. 만일 m번째 위치에서 나눌 수 있다면 각 길이가 m, n인 두 개의 막대로 나눌 수 있고 이때의 경우의 수는 f_mf_n입니다. 길이가 2인 타일이 m, m+1에 위치하여 m번째에서 나눌 수 없다면 길이가 m-1, n-1인 두 개의 막대로 나눌 수 있습니다. 이때의 경우의 수는 f_m-1f_n-1입니다.

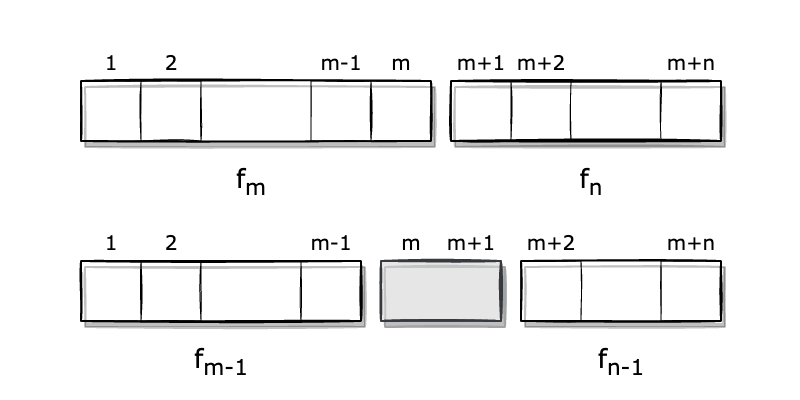
이때 발생한 두 가지 경우의 수 f_mf_n와 f_m-1f_n-1를 더하면 완벽하게 m+n 타일링에 대응됩니다.

2. Dynamic Programing

위에서 사용한 내용은 주로 알고리즘에서 Dynamic Programing의 형태로 나타납니다. 프로그래머스나 백준, leetcode 등에서도 해당 타일링을 응용한 문제를 어렵지 않게 발견할 수 있습니다.

2.1 [2 × n 타일링] - 프로그래머스

바로가기

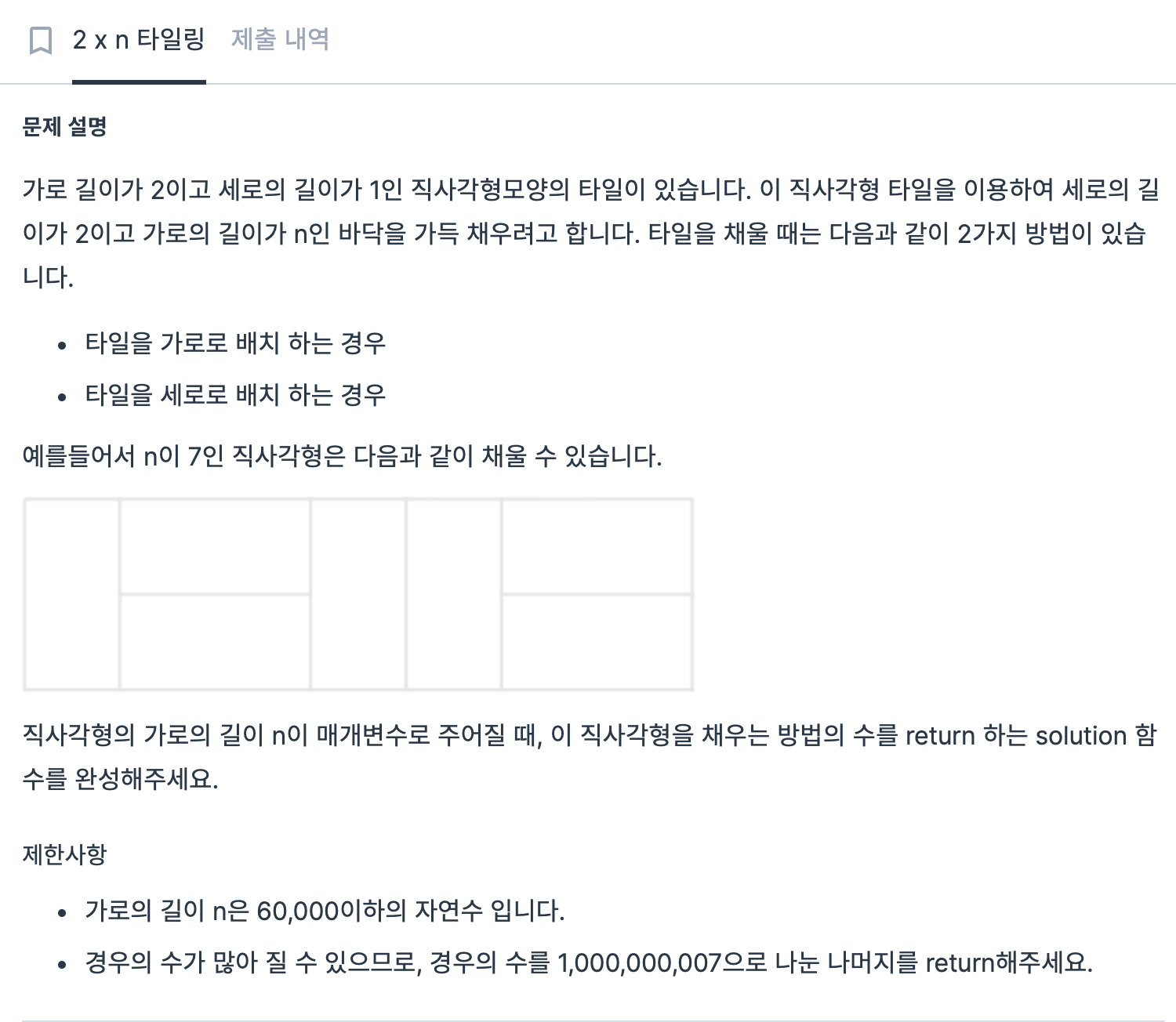
타일을 채우는 방식이 세로로 하나씩 채우거나 가로 방향으로 두 개를 채우는 방법밖에 없는데, 사실상 위에서 알아본 1xn크기의 막대를 채우는 타일링과 완벽히 일치합니다.

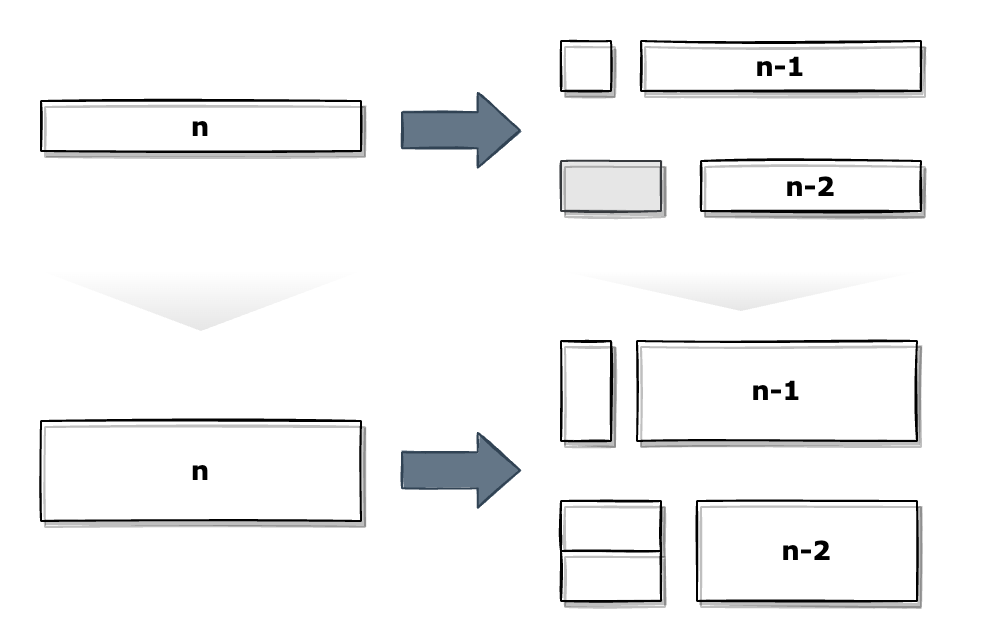
이런 방식을 구현해보면 파이썬을 사용한 경우 아래와 같이 작성할 수 있습니다.

def solution(n: int):
    a, b = 1, 1
    for _ in range(n-1):
        a, b = b, (a+b) % 1000000007
    return b

2.2 [타일링] - 백준 1793

바로가기

해당 경우는 아래와 같은 세 가지 경우로 나누어 생각해 볼 수 있습니다.

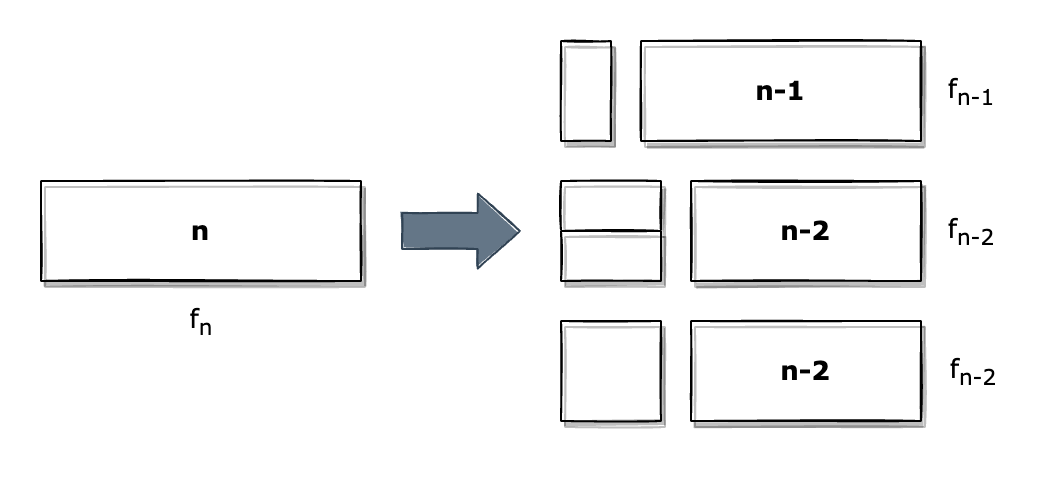
첫번째 타일은 반드시 다음 세가지 중 하나입니다.

2x1 타일을 세로로 두거나,
2x1 타일 두 개를 가로롤 채우거나
2x2 타일을 채우거나

이때 길이가 n인 직사각형을 채우는 경우의 수를 f_n이라고 할 때 나머지 직사각형을 채우는 경우의 수는 각각 f_n-1, f_n-2, f_n-2 입니다. 따라서 아래와 같은 공식이 성립합니다.

f_n = 2f_n-1 + f_n-2

해당 내용을 바탕으로 결과를 작성해보면 아래와 같습니다.

def solution(n: int):
    a, b = 1, 1
    for _ in range(n-1):
        a, b = b, 2*a + b
    return b

References

Arthur T. Benjamin and Jennifer J. Quinn, Proofs that Really Count: the Art of Combinatorial Proof, Mathematical Association of America, 2003-07

[알고리즘] 타일링